PERMUTASI
Coba perhatikan contoh-contoh di bawah untuk memahami Permutasi dalam konsep Peluang pada pelajaran Matematika.
Contoh I:
{a,b,c}
Jika dipilih 2 dari 3 unsur tersebut, maka banyaknya permutasi dari 3 unsur setiap pengambilan 2 unsur adalah 6, yaitu ab, ba, ac, ca, bc, cb.
Ditulis 3P2 = 6.
Contoh II:
{a,b,c}
maka, banyaknya permutasi dari 3 unusr setiap pengambilan 3 unsur adalah 6, yaitu abc, acb, bac, bca, cab, cba.
Ditulis 3P3 = 6
RUMUS
Catatan: Notasi Faktorial
3! = 3x2x1
5! = 5x4x3x2x1
1! = 1
Def 0! = 1
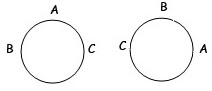
Permutasi Siklis
{a,b,c}
Maka, jika menggunakan permutasi siklis, hasil dari pengambilan 3 unsur dari 3 unsur dapat digambarkan seperti gambar di samping.
RUMUS: banyaknya permutasi = (n-1)!
KOMBINASI
Contoh III:
{a,b,c}, pengambilan 2 unsur dari 3 unsur.
menggunakan kombinasi maka akan diperoleh hasil kombinasinya ab, bc, ca.
Ditulis 3C2.
RUMUS
PERBEDAAN KOMBINASI DAN PERMUTASI
Salah satu perbedaan antara Permutasi dan Kombinasi adalah jika Permutasi maka perbedaan urutan menjadikan perbedaan makna, sementara di Kombinasi perbedaan urutan tidak akan menjadikan perbedaan makna. Contoh: {a,b,c} pengambilan 2 unsur dari 3 unsur jika menggunakan permutasi maka akan diperoleh hasil ab, ba, ac, ca, bc, cb.
Tetapi jika menggunakan kombinasi hasil yang diperoleh adalah ab, ca, bc.
Contoh lain permutasi:
ada nomor kendaraan di Indonesia yaitu AB (Jogjakarta dan sekitarnya), tetapi apabila dibalik maka menjadi BA (Padang), maka terlihat perbedaan maknanya.
Contoh lain kombinasi:
 Ada dua titik A dan B, dihubungkan oleh satu garis.
Ada dua titik A dan B, dihubungkan oleh satu garis.
Maka garis AB = BA, yang berarti tidak menyebabkan perbedaan makna.
Coba perhatikan contoh-contoh di bawah untuk memahami Permutasi dalam konsep Peluang pada pelajaran Matematika.
Contoh I:
{a,b,c}
Jika dipilih 2 dari 3 unsur tersebut, maka banyaknya permutasi dari 3 unsur setiap pengambilan 2 unsur adalah 6, yaitu ab, ba, ac, ca, bc, cb.
Ditulis 3P2 = 6.
Contoh II:
{a,b,c}
maka, banyaknya permutasi dari 3 unusr setiap pengambilan 3 unsur adalah 6, yaitu abc, acb, bac, bca, cab, cba.
Ditulis 3P3 = 6
RUMUS
Catatan: Notasi Faktorial
3! = 3x2x1
5! = 5x4x3x2x1
1! = 1
Def 0! = 1
Permutasi Siklis
{a,b,c}
Maka, jika menggunakan permutasi siklis, hasil dari pengambilan 3 unsur dari 3 unsur dapat digambarkan seperti gambar di samping.
RUMUS: banyaknya permutasi = (n-1)!
KOMBINASI
Contoh III:
{a,b,c}, pengambilan 2 unsur dari 3 unsur.
menggunakan kombinasi maka akan diperoleh hasil kombinasinya ab, bc, ca.
Ditulis 3C2.
RUMUS
PERBEDAAN KOMBINASI DAN PERMUTASI
Salah satu perbedaan antara Permutasi dan Kombinasi adalah jika Permutasi maka perbedaan urutan menjadikan perbedaan makna, sementara di Kombinasi perbedaan urutan tidak akan menjadikan perbedaan makna. Contoh: {a,b,c} pengambilan 2 unsur dari 3 unsur jika menggunakan permutasi maka akan diperoleh hasil ab, ba, ac, ca, bc, cb.
Tetapi jika menggunakan kombinasi hasil yang diperoleh adalah ab, ca, bc.
Contoh lain permutasi:
ada nomor kendaraan di Indonesia yaitu AB (Jogjakarta dan sekitarnya), tetapi apabila dibalik maka menjadi BA (Padang), maka terlihat perbedaan maknanya.
Contoh lain kombinasi:
 Ada dua titik A dan B, dihubungkan oleh satu garis.
Ada dua titik A dan B, dihubungkan oleh satu garis.Maka garis AB = BA, yang berarti tidak menyebabkan perbedaan makna.




THANKS TULISANYA
ReplyDeleteSALAM KENAL
terima kasih ats penjelasannya pak :)
ReplyDelete3P3 kok hasilnya sama 3P2. Mohon penjelasannya
ReplyDelete@Anonymous
ReplyDeleteYa hasilnya sama,
oke, mari kita coba kerjakan yaaa, :D
nPr = n!/{n-r)!
Supaya lebih jelas liat
sini
maka untuk 3P2
3P2 = 3!/(3-2)! = 6/1 = 6
lebih jelas --> nih liat
dan untuk 3P3
3P3 = 3!/(3-3)! = 6/0! = 6/1 = 6
lebih jelas lagi di sini
catatan, untuk 0! = 1 (sudah saya tuliskan di atas kok)
jadi begitu. :)
semoga membantu. :D